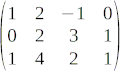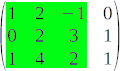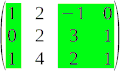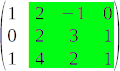Aquesta secció recull mètodes per fer la invers d'una matriu.
Per fer aquest tipus d'inversa es necessiten petites eines o conceptes per obtenir una visió simplista i ràpida del que és la inversa amb menors.
El menor complementari de  de la matriu
de la matriu  és el determinant:
és el determinant: 
L'adjunt de  de la matriu
de la matriu 
Tenint en compte els signes següents:

és el determinant 
Menors de diferent ordre
edit
Aquí parlem en plural ja que es tracta d'identificar-los simplement.
Els menors d'ordre 1 d'una matriu són tots els seus elements. Si la matriu és  llavors té 15 menors d'ordre 1 sense importar si es repeteixen.
llavors té 15 menors d'ordre 1 sense importar si es repeteixen.
Els menors d'ordre 2 d'una matriu són tots els determinants de matrius  que podem obtenir eliminant les files i columnes que siguin necessàries.
que podem obtenir eliminant les files i columnes que siguin necessàries.

Els menors d'ordre 3 d'una matriu són tots els determinants de matrius  que podem obtenir eliminant les files i columnes que siguin necessàries.
que podem obtenir eliminant les files i columnes que siguin necessàries.
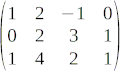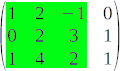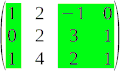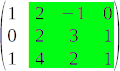
I així successivament per als menors d'ordre superior.
Càlcul de rang per menors
edit
Per calcular el rang només cal buscar el menor més gran possible que no sigui zero, llavors l'ordre d'aquest menor és el rang.
- S'ha de començar pels menors d'ordre més grans i, si tots són zero, continuar la recerca dels següents menors d'ordre inferior.
Adjunta d'una matriu
edit
L'adjunta d'una matriu quadrada és una nova matriu del mateix ordre, on els elements ara són els adjunts dels elements anteriors i un signe  , per exemple i com a similitud de:
, per exemple i com a similitud de:
Donada la matriu  llavors:
llavors: 
tenim:
 llavors:
llavors: 


Per aquest càlcul es fa servir la fórmula: 
Exercici:
Calculeu amb aquest mètode la inversa de les matrius:
a) 
b) 
c) 
d) 
e)